في عام 2010، ألقى إدوارد ويتن محاضرة لعامة الناس نيابة عن IAS (معهد الدراسات المتقدمة في الولايات المتحدة الأمريكية) حول نظرية التشابك وميكانيكا الكم. وفي هذا المقال سننقل النقاط الرئيسية لكلماته مع امتدادات محددة. في ظاهر الأمر، بدأت نظرية الترابط باعتبارها "خدعة" رياضية أخرى، ولكن مثل معظم الاكتشافات العلمية، سبق علماء الرياضيات علماء الفيزياء بعدة عقود

الربط والتحضير هي عمليات روتينية. يقوم الكثير منا كل يوم بربط أربطة الحذاء للسماح لرباط الحذاء بالقيام بعمله - وهو ربط جوانب الحذاء بإحكام. من حين لآخر يأتي الاتصال على حسابنا - من منا لم يشعر بالإحباط عندما اكتشف أن سماعات الرأس السلكية الموجودة في جيبه متشابكة معًا أو أن قطعة المجوهرات الرقيقة التي اشتراها للتو ملتوية بشكل طبيعي وتشكلت بإحكام سندات. التحدي، بالطبع، هو فك الروابط، الأمر الذي يتطلب الكثير من الجهد والكثير من الوقت.
بالنسبة لعلماء الرياضيات، مصطلح "الاتصال" أكثر تجريدًا ولكنه في المجمل يصف حلقة تطفو بحرية في الزمكان. يظهر مثال أساسي للعقدة في الشكل رقم 1، آمل أن يذكرك هذا الشكل بخيط ملتوي من الحياة اليومية. إذا كانت الصورة مربكة، فلا تقلق، فأنت لست الوحيد. يجد العديد من علماء الرياضيات صعوبة في فهم كيفية تكرار الاتصالات وكيفية مقارنتها. يريد الكثير منا (وليس علماء الرياضيات فقط) أن يعرفوا مسبقًا أي العلاقات لا يمكن تحضيرها قبل البدء في العمل الشاق (من الواضح أن هذا عار على هذا الجهد). هذا سؤال غير تافه حقًا، وبالتالي فهو دافع إيجابي لبناء نظرية الروابط.
ولكن مهلا، قطع العلاقات؟ كيف يرتبط كل هذا بالرياضيات؟ إلى آذان أولئك الذين اعتادوا على الاعتقاد بأن الرياضيات ليست أكثر من الجمع والطرح والضرب والقسمة، تظهر في أذهانهم عدد لا بأس به من علامات الاستفهام. في الواقع، قام علماء الرياضيات في القرن العشرين ببناء نظرية أساسية وعميقة على الروابط فقط. ولكن لماذا يهتم الفيزيائيون بنظرية الروابط، إلى جانب المتعة الواضحة في حل الألغاز المسلية؟ بدأ الاهتمام ببعض الاكتشافات المفاجئة منذ بضعة عقود مضت، ولكي نصفها بشكل صحيح، سنبدأ بشرح بسيط لـ "متعددات حدود جونز" التي تم اكتشافها عام 1983. والأمر المدهش هو أن الفكرة يمكن شرحها أيضًا لطلاب المدارس الثانوية وهو أمر لا يكاد يوجد في الرياضيات الحديثة. لتوضيح مدى دهشة هذا الأمر، فكر في احتمالية قيام شخص ما بمحاولة شرح نظرية فيرما الأخيرة لفتيات وفتيان بعمر 16 عامًا.

من أجل البساطة، يُزعم أن جونز أرفق رقمًا (أو متعدد الحدود) بكل رابطة. لنفترض أن لدينا بعض الارتباطات تسمى K وسنصف رقم جونز المرتبط به بالرمز JK. لحساب رقم جونز، كل ما عليك فعله هو تشغيل الوصفة الآمنة التي يمكننا من خلالها حساب قيمته بقليل من الصبر. إذا جK يساوي 1، نحدد أنه لا يوجد اتصال في الحلقة (الشكل 2).

أي رقم آخر غير واحد سوف يعني أن العلاقة K ليست أولية. بمعنى آخر، إذا عدنا إلى العلاقة في الشكل 1، يكاد يكون من المستحيل معرفة كيف يمكن تحضير هذه العلاقة، ولكن بفضل جونز يمكن تحديد هذه الحقيقة، يتعين على المرء ببساطة حساب قيمة JK . إذا كان مختلفًا عن الآخر، فلا يمكن التراجع عن الاتصال. الطريقة التي وصل بها جونز إلى قيمة JK معقدة للغاية، ولكن بمجرد أن نحصل على الطريق، لا تحتاج إلى أن تكون متطورًا لحسابها. لنكون صادقين، هناك عدة طرق لحساب رقم جونز، وفي هذه المقالة سنرى طريقة واحدة. لكل اتصال ليس في الشكل 2، سيتعين علينا "لعب" اللعبة التالية - اختر أرقامك الثلاثة المفضلة، دعنا نقول 2,3,5،3،XNUMX. الآن دعونا نلقي نظرة على الاتصال الجزئي (الشكل XNUMX)، فهو جزئي لأنه يحتوي على جزء مفقود.

إذا فكرت في الأمر للحظة، فهناك ثلاثة خيارات لإكمال الجزء المفقود (الشكل 4).
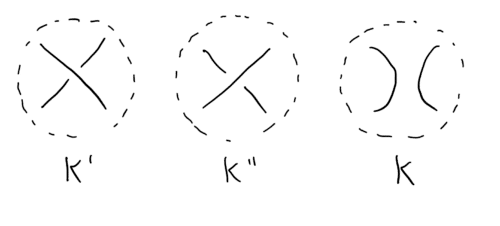
سنضع علامة على كل خيار على أنه K، K'، K". أظهر جونز أنه بالنسبة لثلاثة خيارات توجد العلاقة التالية:
2 JK + 3 Jك ' + 5 Jك" = 0.
إذا قمنا بإجراء العديد من التكرارات على حلقات إضافية في هذا الصدد، فيمكننا إجراء الحساب في النهاية JK الأصلي
الطريقة التي وصفناها هنا تنجح بكفاءة عالية في حساب JKولكن لماذا هذا صحيح؟ لسوء الحظ، من الصعب أن أشرح لأولئك الذين ليسوا علماء رياضيات أو فيزيائيين سبب نجاح الوصفة. عادةً ما يجذب الأشخاص من نوع "لماذا" الأشخاص لدراسة الرياضيات، وإذا طرحت هذا السؤال للتو، فربما يتعين عليك دراسة هذا المجال في المستقبل. مباشرة بعد اكتشاف كثيرات حدود جونز، اكتشف العديد من علماء الرياضيات علاقات أكثر غرابة، تلك التي ليس لها تفسير متعمق. وعلى الرغم من كل شيء، ظل التلميح معلقًا في الهواء. بصراحة، كان هناك عدد غير قليل من التلميحات، خاصة من اتجاه الفيزياء الرياضية. على مر السنين، اتضح أن نظرية التشابك لها علاقة عميقة بنظرية الكم، لذلك سنشرح بإيجاز كيف تختلف ميكانيكا الكم عن الميكانيكا الكلاسيكية.
وفقا للميكانيكا الكلاسيكية، يتحرك الجسيم من نقطة إلى أخرى في مسار واحد تحدده القوى المؤثرة عليه (الشكل 5) وفقا لقوانين نيوتن.
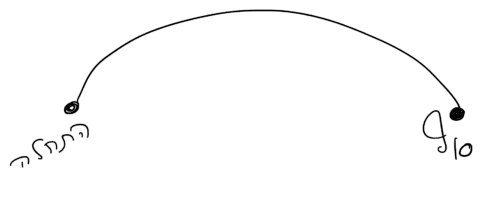

ومن ناحية أخرى، ووفقًا لمبدأ فاينمان، يمكن للجسيم الكمي أن يتحرك في أي مسار، مهما كان غريبًا. يمكن أن يتحرك في المسار الكلاسيكي ولكن أيضًا في مسار متعرج كما في الشكل 6. ويرتبط كل مسار برقم، أو بشكل أكثر دقة، احتمال أن يتحرك الجسيم على هذا المسار. نظرًا لأن الجسيم الكمي يمكن أن يتحرك في أي مسار محتمل، فإنه يمكنه أيضًا التحرك على مسار محدد ومتعرج كما في الشكل 7. يعرف فيزيائي الكم ذو الخبرة كيفية ترجمة أي مسار إلى احتمال، حتى المسار مثل ذلك الموضح في الشكل 7 أو 6، مع أنها أقل احتمالاً من المسار الكلاسيكي. يتطلب الحساب الكثير من الجهد وأدوات تحليلية قوية. بشكل عام، يمكن حساب احتمالية كل مسار K بواسطة مشغل ويلسون المشار إليه بـ Wk. وفي إطار المقال لن نتمكن من تعريفه ببساطة، ولكن لجميع الاحتياجات العملية يقال إن مشغل ويلسون هو أداة مهمة وأساسية في نظرية الكم، على سبيل المثال يستخدم لوصف قوة العامل. القوى بين الكواركات. إذا كان الأمر كذلك، فقد اتضح أن العلاقة بين كثيرات حدود جونز ونظرية الكم تنبع من حقيقة أن المتوسط الكمي لمشغل ويلسون على مدار ملتوي K هو JK ! هذه نتيجة بسيطة ورائعة بالنظر إلى العمل الذي يتطلب الكثير من الجهد التحليلي لحساب كل احتمال.
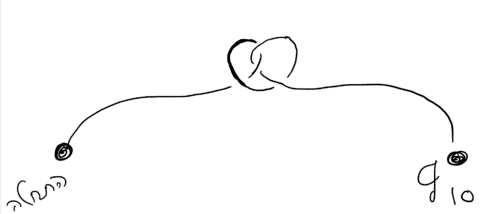
كما يأتي الوصف الرائع والمثير للدهشة بجانبه علامة النجمة - فالاتصالات التي اعتدنا على تخيلها موجودة في الفضاء ثلاثي الأبعاد، ولكن عندما تؤخذ نظرية الكم في الاعتبار، يجب أن نفترض أن الاتصالات تطفو في الزمكان. ولتحقيق هذه الغاية، طور هوبانوف رياضيات غير تافهة تعمل على توسيع متعددات حدود جونز إلى الفضاء ثلاثي الأبعاد بالإضافة إلى البعد الزمني. فكرة هوفانوف أكثر تجريدًا من الرقم الذي يصف الروابط والأغطية. في الواقع، ربط هوفانوف الحالات الكمومية بالدوران، وبمساعدتها، يمكن حساب الخصائص الفريدة للمواد في الطبيعة. وبتعبير أدق، فإن المسارات المتصلة والمتعرجة التي تتحرك بها الجسيمات مهمة جدًا في نظرية المجال الكمي الطوبولوجي، وكمثال على ذلك، يعتبر نموذج تشيرن سيمونز هو النموذج الأكثر نجاحًا في السنوات الأخيرة. يمكن كتابة سلسلة منفصلة من المقالات حول النموذج، ولكن إذا أشرنا إليه باختصار، فإن النموذج يأخذ في الاعتبار الخصائص الطوبولوجية الفريدة التي يمكن استخدامها لشرح، على سبيل المثال، تأثير هول الجزئي.
في الختام، غالبًا ما تسبق الرياضيات الفيزياء، ولكن تمامًا مثل نظرية التشابك وميكانيكا الكم، ينكشف الجمال الحقيقي عندما تنجح الرياضيات في وصف العالم المادي.
إلى المحاضرة الأصلية على يوتيوب
المزيد عن الموضوع على موقع العلوم:

تعليقات 2
ستنتقل معظم الجزيئات من نقطة إلى أخرى كما في الشكل 5
هناك جزيئات لها الرغبة والقدرة والطموحات وهذه ستنتقل من نقطة إلى أخرى بطريقة ملتوية مختلفة وغير متوقعة - لأنها تريد وتستطيع
مثل طائر النورس جوناثان ليفنجستون - تنضم هذه الجسيمات إلى مثيلاتها وتخلق عالمًا ملونًا ومثيرًا للاهتمام ومألوفًا
كما أن هناك جسيمات موضوعية تراقب من الجانب ومن وقت لآخر تختار مسار الحركة أي المسار من نقطة إلى أخرى
يبقى البعض كمتفرجين، والبعض الآخر يريد التحرك كما في الشكل 5 دون جهد، والبعض يختار التحرك بشكل مختلف ويفشل
ويعودون للمشاهدة من الخطوط الجانبية حتى الاندفاع التالي، ومنهم من يحاول مراراً وتكراراً وتكراراً تباعاً حتى يتمكن من التحرك في الطريق الذي اختاره
ومن يملك الإرادة والقدرة والطموح ينجح في الانضمام فوراً إلى نوعه وتكوين روابط حركية معقدة... و استمتع
في الشكل 4 هناك خيار بسيط آخر. بالطبع هناك خيارات معقدة أخرى لا حصر لها - لف الخيوط مرة، مرتين، مليون مرة.