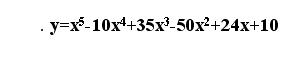الحث البيولوجي، الحث الرياضي

الدكتور ابراهام بن عزرا

الرابط المباشر لهذه الصفحة: https://www.hayadan.org.il/benezrabioint.html

الاستقراء البيولوجي: اليوم أشرقت الشمس، وأمس أشرقت الشمس، وأول أمس أشرقت الشمس، وهكذا كل يوم ننظر إلى الوراء إلى ما وصلت إليه معرفتنا.
الخلاصة: غداً ستشرق الشمس.

אינדוקציה מתמטית: אם בבדיקה עבור n=1 ו- n=2 הכלל המתמטי הרשום כשהוא כולל את n (מספר טבעי) – נכון, ובנוסף, בהנחה כי הכלל נכון לגבי n מוכח כי הוא נכון גם לגבי n+1, אזי הכלל הרשום הוא صحيح.

وهذا يعني أنه في الرياضيات، الخبرة ليست برهانًا، والدليل الرياضي البحت مطلوب.
يبدو أحيانًا لمن ليس على دراية بنظرية الرياضيات أن علماء الرياضيات يراكمون على أنفسهم صعوبات غير ضرورية تتجاوز ما هو ضروري، لأنه إذا كانت معادلة معينة صحيحة، أو قاعدة معينة صحيحة، فيما يتعلق بسلسلة طويلة جدًا من العمليات الخاصة الحالات - فالأفضل قبول القاعدة [أو المعادلة] على أنها حكيمة، حتى لو كان البرهان المحض صعباً نوعاً ما وغير معروف في الحقيقة على الإطلاق.
على سبيل المثال، أرقام مارسان [مارين مارسان، عالم الرياضيات الفرنسي الذي ابتكر في القرن السابع عشر]، وصيغتها العامة هي: 2ن-1، حيث n عدد طبيعي. دعونا نختبر فرضية مفادها أنه عندما يكون n عددًا أوليًا، فإن رقم مارسان المقابل يكون أوليًا أيضًا.
[العدد الطبيعي هو عدد موجب وصحيح. العدد الأولي هو عدد طبيعي غير قابل للقسمة (بدون باقي) إلا على نفسه وعلى 1، على عكس الرقم المركب الذي يقبل القسمة على عدة أرقام. وبطبيعة الحال، كل رقم زوجي باستثناء 2 هو رقم معقد أيضًا].
وبدراسة الفرضية السابقة نحصل على نتائج إيجابية كما يلي:

وهو ما يناقض فرضية أويلر، لأن هنا مجموع أربع قوى إلى الدرجة الخامسة يعطي عددا هو قوة خامسة.

وفيما يلي شرح لكيفية إنشاء معادلة لن تفاجئ الربيع إلا بعد عدد كبير من المحاولات، كما نريد.

دعونا نفحص المعادلة أدناه:

وتحقق، ما هي قيمة y لـ x تساوي 0، 1، 2، إلخ.

سوف نثبت أنه بالنسبة لـ x=0 نحصل على y=10، ومن المثير للدهشة أيضًا أنه بالنسبة لـ x=1 x=2 x=3 x=4
يتم الحصول على نفس النتائج - ص = 10.

لا ينبغي لنا أن نستنتج أنه علاوة على ذلك، بالنسبة للأعداد الطبيعية، سيتم الحصول على نفس النتيجة، لأن هذا قد تم انتهاكه بالفعل بالنسبة لـ x=5.

والسبب في ذلك يكمن في الحقيقة الرياضية المتمثلة في أنه يمكن أيضًا كتابة المعادلة نفسها على النحو التالي:

. y=10+x[(x-1)(x-2)(x-3)(x-4)]

ومن هذا يتبين أنه بالنسبة لجميع قيم x من صفر إلى 4 في الأعداد الصحيحة يكون الناتج واحد y=10، وذلك في ظل إعادة ضبط الحد المركب للمعادلة في كل هذه الحالات. وبالطبع بنفس الطريقة، إذا أردنا أن نكتب معادلة يكون فيها x=0 إلى x=1000000 بأعداد صحيحة، فإن جميع النتائج ستكون y=10 - لا يوجد شيء أبسط من ذلك، وهنا معادلة:

.y=10+x[(x-1)(x-2).. ..(x-1000000)]

وفيما يتعلق بجميع القيم من صفر إلى 1000000 في الأعداد الصحيحة، فإن جميع النتائج ستكون y=10، ومن الواضح أنه بالنسبة لأي قيمة x أكبر من 1000000 فإن قيمة y ستكون مختلفة عن 10، ولن نكون كذلك قادرة على احتواء الاستدلال هنا وفق الاستقراء الطبيعي مطلقا...

عبقري الرياضيات
https://www.hayadan.org.il/BuildaGate4/general2/data_card.php?Cat=~~~864195693~~~133&SiteName=hayadan